Background
Accounting Standard 15 (and its 2005) revision, Indian Accounting Standard 19 (Ind AS 19) mandate an entity registered in India to execute actuarial valuations of employee benefit plans.
In the Indian landscape, plans which typically fall under the ambit are:
- gratuity (as applicable by law)
- leave encashment (earned leave, privilege leave), sick and/or casual leave (if allowed to carried forward),
- defined benefit pension (schemes are run typically by PSUs and legacy conglomerates)
- retirement award/long service award/long service benefit (benefit paid in cash (or kind) upon completion of certain service milestones and on retirement)
- long term incentive plans (cash incentives, given meeting of a performance criteria)
Typically, in most startups, small & medium sized organizations, gratuity and leave encashment for which valuations are carried about using actuarial methods.
The key assumption used in the actuarial valuation is the discount rate.
Bond yields
Discount rate is a critical assumption. Let’s first consider why.
Actuarial liabilities are arrived at using Projected Unit Credit Method (PUCM). In simple terms, the method involves projecting cash outflows expected to occur over long periods of time in the future. For a relatively young organization, these projections could span over two or three decades on average for each employee. For example, for a 35-year-old employee, the projections of expected future cash outflows would span over 25 years assuming a retirement age of 60 years.
Since we are working with liabilities expected to arise far out in the future, there is a need to determine these liabilities in present day values using a discount rate. Thus making the discount rate a critical assumption. Further, a single rate is used to discount all future expected cash outflows for all employees in an organization.
Both accounting standards require the discount rate to be based on govt. bond yields as on the balance sheet date. As govt. bonds are risk-free, we’re considering the risk-free rate of return without any explicit loading to discount future payments.
According to Para 83 of Ind AS 19 – The rate used to discount post-employment benefit obligations (both funded and unfunded) shall be determined by reference to market yields at the end of the reporting period on government bonds.
Govt. bond yields are published on daily basis on various platforms. We prefer to use the rates published publicly by the Clearing Corporation of India. A graphical representation of a yield curve, on various dates looks like this.
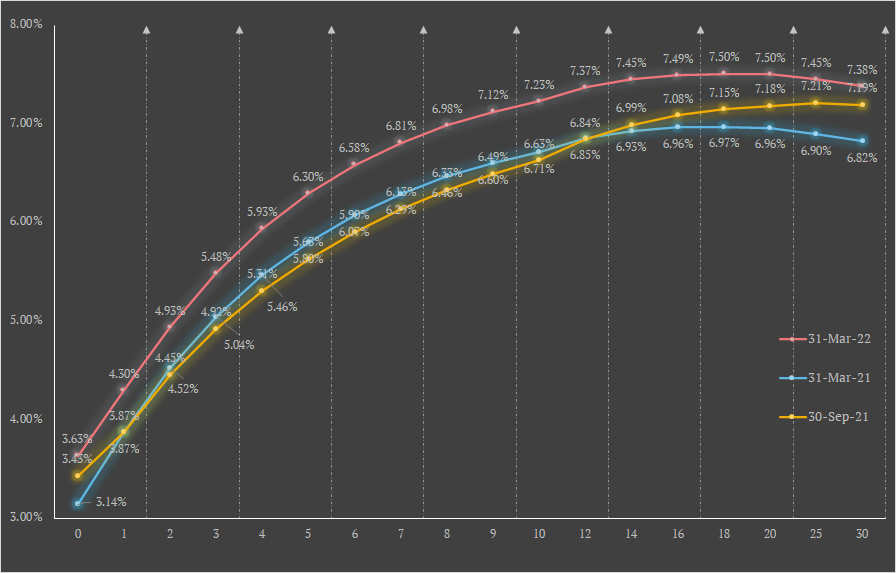
The yields vary over the tenure of the bonds. Yields on a long term bonds typically reward higher than short term bonds as investors have tied up their monies for longer periods. As seen above, the yield curves are upward sloping and hence a 3-year-bond fetches a (significantly) different yield than an 8-year-bond.
To make matters simple, the standards do not suggest to use the yields across the entire curve to discount future liabilities. The yield applicable on a particular term would suffice. This poses the question, which term on the curve should one refer to?
The answer lies in para 83 of Ind AS 19 – the currency and term of the government bonds or corporate bonds shall be consistent with the currency and estimated term of the post-employment benefit obligations.
A few things to take note of
- a) the currency of the liabilities have to match with the currency of the bonds.
- b) the term of the govt. bonds have to be consistent with the estimated term of the post-employment benefit obligations.
Post employment term of benefit obligations
During the audit process, more often than not, we get comment stating that the duration of the bond yields should be derived as;
$$ duration = average\,age\,of\,the\,employees\,-\,retirement\, age.$$
Therefore, if the average age of employees in a given entity is 33 years, given a retirement age of 60 years the duration works out to 27 years. Thus, the yield corresponding to 27 years on the yield curve is to be considered as the discount rate.
The above and other probability-based metrics measuring the expected tenure or expected future service of the employees are, in our view, inconsistent with the term estimated term of the post-employment benefit obligations as suggested by the standards.
Say, in a gratuity actuarial valuation of a 35 year-old-employee, the estimated term of the gratuity obligation is different than the estimated term till retirement. We are looking for the estimated term of the obligation and not estimated term of the employee’s future tenure.
Macaulay’s Duration
Macaulay’s Duration, often referred to as Duration, is a key principle in the fixed-income investment world. The idea was first put forward by Frederick Macaulay in 1938, and what was invented back then became hugely important for the market as it allows us to understand the behavior of bonds in the given context of the interest rates changes.
In simple terms, weighted averages of cash flows, arising during the tenure of the bond, are considered, and then the weighted sum of averages is taken out, which gives us the final answer. The formula is as follows:
$$Duration = n\bigg\{\frac{F}{(1+y)^n} \bigg\}+ \sum_{i=1}^{n} i * \bigg\{ \frac{C_i}{(1+y)^i} \bigg\} $$
$F$ is the face value of the bond,
$C_i$ is the coupon payments at time $i$,
$y$ is the yield-to-maturity,
$P$ is the price of the bond.
The terms in the curly brackets are cashflows which are weighted with the time when they arise.
Duration is expressed in years. It is thought of as the economic balance point where the present value of bond’s future cashflows equal to the amount paid for the bond.
Duration is critical to bond portfolio management. It helps benchmark bonds, aids in managing interest rate risk, and helps the investor to protect the portfolio from interest rate fluctuations.
Let us revisit term post employment term of benefit obligations used by the accounting standards.
Essentially, we are looking for the economic balance point wherein, provision held today in the books, match with the present value of expected future benefit obligations posed by the employees.
Duration, as a metric, comes closest to capturing the essence of the term estimated term of benefit obligations. Instead of using a bond’s future cashflows, we consider the future benefit obligations posed by an employee in the duration formula and we get estimated term of benefit obligations. Mathematically,
$$estimated\,term\,of\,benefit\,obligations = \sum_{t=1}^{n} t * \bigg\{ \frac{DBO_t}{(1+d)^t} \bigg\} $$
$d$ is the discount rate,
$DBO_t$ is the defined benefit obligation posed by an employee at time $t$
Duration is calculated for each employee in the cohort and subsequently an entity-level average is derived.
In this context, Duration can be interpreted as expected average tenure of outstanding liabilities. As the DBO is arrived using assumptions such as discount rate, salary escalation rate, attrition & mortality rates, duration captures the impact of all actuarial assumptions considered in the valuation.
As established earlier, (expected) future tenure of the employee is a different quantity than expected future tenure of the DBO posed by the same employee. Thus, duration captures not only the future potential service of each employee, but also the sensitivity of the employee’s liability to actuarial assumptions.
Therefore, in an actuarial valuation in an Indian context, the approach is to derive duration employee-wise and the entire cohort and then trace the corresponding g-sec yield as on the date of the balance sheet. For example, if the overall duration of DBO works out to 8.75 years, then we linear interpolate the yields of 8-year and 10-year bonds and derive the discount rate.